一、问题重述
问题重述部分是要保持全文的完整性,要求用自己的语言将赛题重述一遍,可以简单地有删有增地重述,注意:拟解决的问题不得省略.
l 论文(答卷)用白色A4纸,上下左右各留出2.5厘米的页边距。
l 论文第一页为承诺书,具体内容和格式见本规范第二页。
l 论文第二页为编号专用页,用于赛区和全国评阅前后对论文进行编号,具体内容和格式见本规范第三页。
l 论文题目和摘要写在论文第三页上,从第四页开始是论文正文。
l 论文从第四页开始编写页码,页码必须位于每页页脚中部,用阿拉伯数字从“1”开始连续编号。
l 论文不能有页眉,论文中不能有任何可能显示答题人身份的标志。
l 论文题目用3号黑体字、一级标题用4号黑体字,并居中。论文中其他汉字一律采用小4号黑色宋体字,行距用单倍行距。
l 提请大家注意:摘要应该是一份简明扼要的详细摘要(包括关键词),在整篇论文评阅中占有重要权重,请认真书写(注意篇幅不能超过一页,且无需译成英文)。全国评阅时将首先根据摘要和论文整体结构及概貌对论文优劣进行初步筛选。
l 引用别人的成果或其他公开的资料(包括网上查到的资料)必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。正文引用处用方括号标示参考文献的编号,如[1][3]等;引用书籍还必须指出页码。参考文献按正文中的引用次序列出,其中书籍的表述方式为:
l [编号]作者,书名,出版地:出版社,出版年。
l 参考文献中期刊杂志论文的表述方式为:
l [编号]作者,论文名,杂志名,卷期号:起止页码,出版年。
l 参考文献中网上资源的表述方式为:
l [编号]作者,资源标题,网址,访问时间(年月日)。
l 在不违反本规范的前提下,各赛区可以对论文增加其他要求(如在本规范要求的第一页前增加其他页和其他信息,或在论文的最后增加空白页等);从承诺书开始到论文正文结束前,各赛区不得有本规范外的其他要求(否则一律无效)。
二、问题分析
这一部分的任务是对赛题作一全面的分析,说明题目要求解决的是什么问题,解决问题的关键是什么,解决问题的思路、大致步骤,是建立模型之前的必要准备
 要点:弄清题意,梳理解决问题的思路。
要点:弄清题意,梳理解决问题的思路。
在问题分析推导过程要注意的问题:
(1)分析:中肯、确切
(2)术语:专业、内行;;
(3)原理、依据:正确、明确,
(4)表述:简明,关键步骤要列出
忌: 外行话,专业术语不明确,表述混乱,冗长。
注:也可将这一部分归入模型建立
关于如何审题
1、 已知条件有哪些?一一列出
2、 已给的数据有哪些。一一列出。
3、 问题的实际背景是什么?涉及哪些专业术语?其确切含义是什么?
4、 要解决的有几个问题?
每个问题的真实含义是什么?
5、 为了解决这个问题,需要哪些条件与数据?现有条件够不够?现有数据够不够?如果不够,则要补充数据、补充条件假设。
6、 解决某问题的关键是什么?
问题属于哪一类型的数学模型?
问题涉及哪些因素?
7、 如果是优化模型,则要问问题的目标函数是什么?约束条件是什么?要注意将定性的要求转换为定量的方式。
8、 如果问题涉及动态的,则要用微分方程或差分方程的方法。
9、 如果涉及评价,则要用评价的各种方法。
10、 如果涉及不确定因素,则要用到概率统计、模糊数学、灰色系统等等。
三、符号说明
| 符号 |
含义 |
单位 |
备注 |
| 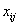
|
第i年发生第j次地震的月份 |
次 |
变量 |
| 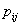
|
第i年发生第j次地震的震级 |
|
|
| 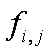
|
第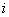 次地震发生时间与第j次地震发生时间之间的间隔 次地震发生时间与第j次地震发生时间之间的间隔 |
年 |
范围:0-25 |
| |
|
|
|
四、模型假设
如何作假设?
原则:对于与问题有关的各个方面(涉及因素)均要作假设。
1.从已知条件中作假设
2.从补充条件中作假设
3.从现实情况出发作假设
4.如果是为了简化模型的计算而作的假设,则必须在模型优缺点中加以说明,并在模型的改进中进行适当分析。
假设分类:
1.全局性的假设(对所有问题均适用)
2、局部性的假设(只对某个问题适用)
注:作假设要切合题意,
关键性假设不可缺,
不要罗列一大堆无用的假设。
五、模型建立
每一篇论文都必须有一个模型!
常见问题:很多参赛队的论文通篇没有一个模型,只是用凑的办法弄出一个结果
数学模型:可以是一个(组)公式、算法、图表等数学结构。
基本模型:
通常是解决问题的一般模型。基本模型要求正确、完整、简洁。
简化模型
当基本模型过于复杂难于求解时,可采用简化模型。
1) 要明确说明:简化思想,依据
2) 简化后模型,尽可能完整给出
模型的选择
(1)模型要实用,有效,以解决问题有效为原则。
(2)数学建模要解决的是实际问题,不追求数学上:高(级)、深(刻)、难(度大)。
能用初等方法解决的,就不用高等方法;
能用简单方法解决的,就不用复杂方法;
能用被更多人看懂、理解的方法,就不用只 能少数人看懂、理解的方法。
竞赛中常见的模型
优化模型、预测模型、描述模型、仿真模型、效用模型、层次分析模型、随机模型、离散模型。
赛题趋势:开放性更强,没有标准答案
公式推导:引用别人的公式则在参考文献中体现出来,自己创作的公式则应加以推导。
六、模型求解
计算方法设计或选择;
算法设计或选择, 算法思想依据,步骤及实现,计算框图;
所采用的软件名称;
引用或建立必要的数学命题和定理;
求解方案及流程。
模型求解时注意事项:
(1) 需要建立数学命题时,命题叙述要符合数学命题的表述规范,尽可能论证严密。
(2) 需要说明计算方法或算法的原理、思想、依据、步骤。
若采用现有软件,说明采用此软件的理由,软件名称。
(3) 计算过程,中间结果可要可不要的,不要列出,但关键结果不可少。
(4) 设法算出合理的数值结果。
七、模型结果分析
包括:结果表示;结果分析、检验;模型检验及模型修正;灵敏度分析,稳定性分析等等。
(1) 最终数值结果的正确性或合理性是第一位的 ;
(2) 对数值结果或模拟结果进行必要的检验。
结果不正确、不合理、或误差大时,分析原因,对算法、计算方法、或模型进行修正、改进;
(3) 题目中要求回答的问题,数值结果,结论,须一一列出;
(4) 列数据问题:考虑是否需要列出多组数据,或额外数据,对数据进行比较、分析,为各种方案的提出提供依据;
(5) 结果表示:要集中,一目了然,直观,便于比较分析
▲数值结果表示:精心设计表格;可能的话,用图形图表形式
▲求解方案,用图示更好
(6) 必要时对问题解答,作定性或规律性的讨论。
(7)灵敏度分析与稳定性分析
对于结果对原始数据依赖性强的情况,还必须进行灵敏度分析与稳定性分析。
但并非所有的模型都需要作灵敏度分析与稳定性分析的。
八、模型优缺点(或模型评价)
自我评价优点要突出,缺点不回避。
优点从哪找?假设合理,建模方法创新,求解特色等
注:这里的优点简化后可在摘要引用;缺点仅在此说明,摘要中就不要引用了。
九、模型改进方向
由于时间关系,一些改进的思路来不及实现,可指出改进方向。
改变原题要求,重新建模可在此做-一般不推荐改变原题要求。
推广或改进方向时,不要玩弄新数学术语。
参考文献
l 引用别人的成果或其他公开的资料(包括网上查到的资料)必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。正文引用处用方括号标示参考文献的编号,如[1][3]等;引用书籍还必须指出页码。参考文献按正文中的引用次序列出,其中书籍的表述方式为:
[编号]作者,书名,出版地:出版社,出版年。
参考文献中期刊杂志论文的表述方式为:
[编号]作者,论文名,杂志名,卷期号:起止页码,出版年。
参考文献中网上资源的表述方式为:
[编号]作者,资源标题,网址,访问时间(年月日)。
例:
[1]姜启源等.数学模型[M].北京:高等教育出版社,2003
[2]舒康,梁镇韩. AHP中的指数标度法[J].系统工程理论与实践,1990,10(1):6-8
[3]卢丽君.老员工数学建模竞赛魅力何在?
http://www.mcm.edu.cn/news/ChinaEdu20060113.htm, 2011-9-8
附录
附录内容:
程序清单,详细数值结果,详细公式推导、定理证明,更多的图表等等
注意事项:
1.结果,数据表格,不要错,错的宁可不列。
2.主要结果数据,应在正文中列出,不怕重复
