“三人同行七十稀，五树梅花二十一，七子团圆正半月，除百零五便得知。”

实际上这个歌谣是一个古老数学题的解法。

韩信点兵

在数学典籍《孙子算经》中，有许多著名的数学问题。其中最有名的是“鸡兔同笼”问题。除此之外，另一个流传很广的经典问题，被后人称为“物不知数”问题：

“有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？”

意思是说：有一堆物体不知道有几个。如果三个三个分组，最后会剩下2个；如果五个五个分组，最后会剩下3个；如果七个七个分组，最后会剩下2个。问这些物体一共有几个？

后来，人们为了让这个问题更具体化，就把它改编成“韩信点兵”问题。

有一次战斗后，韩信要清点士兵的人数。让士兵三人一组，就有两人没法编组；五人一组，就有三人无法编组；七人一组，就有两人无法编组。那么请问这些士兵一共有几人？

宋朝数学家秦九韶在《数书九章》中对这个问题做出了完整系统的解答。明朝数学家程大位在《算法统宗》中将解法编成易于上口的《孙子歌诀》，就是文初的那首歌谣。

同余

现在我们一起来解决这个问题。首先我们来了解一下同余的概念。a和b关于c同余，意思是说a除以c和b除以c的余数相同。例如：8÷5=1余3，3÷5=0余3，所以8和3关于5同余，写作8≡3（mod 5），其中mod读作“模”。而且，由于3小于5，所以3本身就是3除以5的余数，因此8≡3（mod 5）也可以理解为8除以5的余数是3。

这样，韩信点兵问题就可以表示为数学语言了。有一个数字x，除以3余2，除以5余3，除以7余2， 那么这个数字是多少？数学写法是

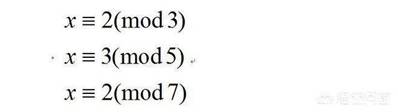
对于这个问题，最基本的解法是穷举法，就是把满足每个条件的数字写出来，然 后找到相同的数字。

除以3余数是2的数字有：2、5、8、11、14、17、20、23、26…除以5余数是3 的数字有：3、8、13、18、23、28…除以7余数是2的数字有：2、9、16、23、30…我们发现，满足三个条件的第一个数字是23。所以23是这个问题的一个解。

但是，这个问题的解并不是唯一的。3、5、7彼此互质，它们的最小公倍数是105。也就是说，105除以3、除以5或者除以7都没有余数。如果一个数字x是满足要求的，那么在x上加上几个105都不会改变它对3、5、7的余数。比如，23是满足要求的，那么23+105=128也是满足要求的，23+210=233也是满足要求的。

所以这个问题最后的解就是23+105n，其中n=0，1，2，3…

歌谣

那么，程大位在《算法统宗》中的歌谣又是什么意思呢？其实这个口诀是一个快速的算法，那就是：

三人同行七十稀：将除以3的余数乘以70；五树梅花二十一：将除以5的余数乘以21；七子团圆正半月：将除以7的余数乘以15（半个月）；除百零五便得知：将以上三个数字相加，最后减去几个105。

例如在“韩信点兵”问题中，除以3的余数是2，除以5的余数是3，除以7的余数是2，那么前三句话就是70×2+21×3+15×2=233，233减去105等于128，128减去105=23，那么23、128、233等就都是这个问题的答案。

这个口诀的证明其实也并不难：

70这个数字是5和7的倍数，并且除以3余1，也就是说，任何一个数添加一个70之后，不会改变除以5和7的余数，但是会在除以3的余数中多1。这样如果所求的数字除以3余2，就应该包含2个70，即70×2。21这个数字是3和7的倍数，并且除以5余1， 也就是说，任何一个数添加了一个21之后不会改变除以3和7的余数，但是会在除以5的余数中多1。这样如果所求的数字除以5余3， 就应该包含3个21，即21×3。15这个数字是3和5的倍数，并且除以7余1， 也就是说，任何一个数添加了一个15之后不会改变除以3和5的余数，但是会在除以7的余数中多1。这样如果所求的数字除以7余2， 就应该包含2个15，即15×2。将以上三个数字相加得到233，就可以得到一个满足条件：除以3余2，除以5余3，除以7余2的数字。105这个数字是3、5、7的公倍数，因此一个数字加上或者减去105之后，不会改变除以3、5、7的余数，因此在刚才得到的233上添加或者减去几个105，都是问题的解。最终，通过口诀我们还是可以得到通解：23+105n，其中n=0，1，2，3…

中国剩余定理

余数问题是一个重要的数学问题，是计算机密码学的基石之一。世界著名的数学家欧拉、高斯等人，都曾经研究过这个问题。中国古代的先贤在这方面取得了丰硕的成果。“韩信点兵”问题只是一个例子，这样的问题有更加普遍和系统化的表示方法。而这个方法，就被世界称为“中国剩余定理”，是我国为数不多的获得世界公认的古代数学成就之一。